Cohen h and h'
Introduction
Cohen h is an effect size measure to compare two proportions (percentages).
Obtaining the Measure
with Flowgorithm
A basic implementation for Cohen Cohen's h' is shown in the flowchart in figure 1
Figure 1
Flowgorithm for Cohen h'

It takes as input the frequency of one of the categories (k) and the sample size (n).
Flowgorithm file: ES - Cohen h2.fprg.
with R
Jupyter Notebook from videos: ES - Cohen h'.ipynb.
with stikpetR
without stikpetR
R file used: ES - Cohen h2.R
Data file used: StudentStatistics.sav
Online calculator
Enter the number of 'successes' (or number of respondents of the first category, the total sample size, and the expected proportion:
Manually (using formula)
The formula for Cohen's h' will be:
\(h'=\phi_{1}-\phi_{c}\)
Where φi is determined by:
\(\phi_{i}=2\times\textup{arcsin}\sqrt{p_{i}}\)
Where pi is the sample proportions of category i, arcsin the inverse sinus function (also known as sin-1), and pc the expected proportion
In the example the female proportion is approximately 0.2609, filling this in for phi (φ) gives:
\(\phi_{1}=2\times\textup{arcsin}\sqrt{0.2609}\approx1.0722\)
For the expected proportion, which was 0.50 we get:
\(\phi_{c}=2\times\textup{arcsin}\sqrt{0.50}\approx1.5708\)
Filling these results in the formula for Cohen's h' we get:
\(h' \approx1.0722-1.5708\approx-0.4986\)
And just for the interpretation, converting this to Cohen's h we get:
\(h\approx-0.4986\times\sqrt{2}\approx-0.7051\)
Interpretation
If you have two percentages, a first idea might be to simply subtract the two from each other, and then derive some rule for saying like a difference of 10% is small, 20% is medium, etc. Lets say you settled on saying that a difference of 10% is small. If one is 45% and the other is 55%, this seems fine. But how about if one is 1% and the other is 11%. Somehow, the difference now seems bigger.
If the percentage is very small, or very large, a smaller difference could be considered bigger, as when both percentages are around 50%. To take this into consideration, Cohen uses a trignonometry function, he took the arcsin of the square root of each of the two proportions, and then determines the difference, and then multiply the result by two, for a range of 0 to pi (Cohen, 1988, p. 181).
Aaron made a great visualisation of Cohen's h and the rule of thumb Cohen proposed. It is copied in figure 1
Figure 1Cohen h Contourplot
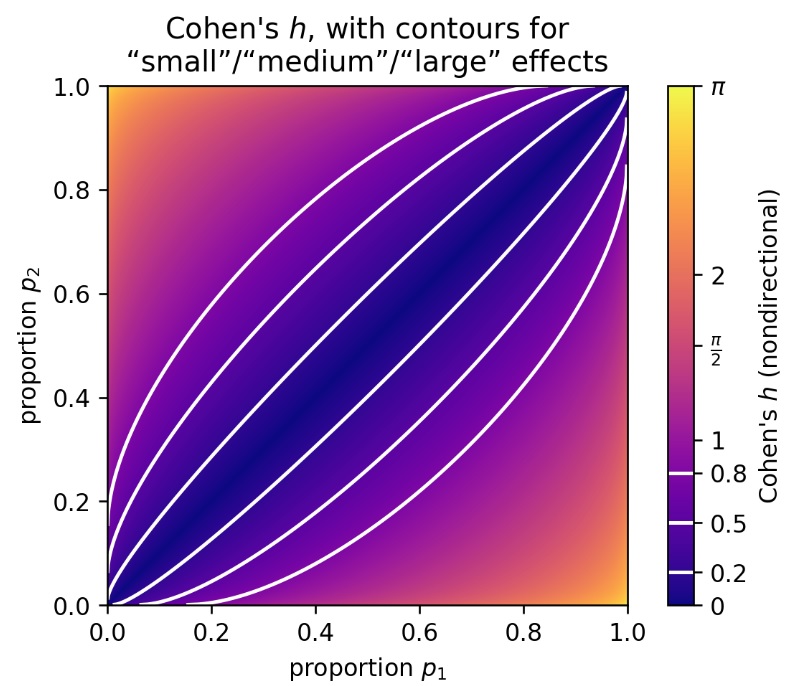
Note: Reprinted from Aaron (https://planspace.org/20211106-visualizing_cohens_h/)
The four white lines in figure 1 are actually two sets, the inner two capture the region where Cohen h will be below 0.2, the ones just out of those the region where h will be below 0.5 and the last is the region for h below 0.8.
Cohen h and h' can range from 0 to \(\pi\). Cohen gives these as rule of thumb for the interpertation (Cohen, 1988, p. 198). They are shown in Table 1.
| |h| | Interpretation |
|---|---|
| 0.00 < 0.20 | Negligible |
| 0.20 < 0.50 | Small |
| 0.50 < 0.80 | Medium |
| 0.80 or more | Large |
| Note: Adapted from Statistical power analysis for the behavioral sciences (2nd ed., p. 198) by J. Cohen, 1988, L. Erlbaum Associates. | |
The above rule-of-thumb can be used if you have two percentages that were tested, however if you only have one percentage that is compared to an hypothesized percentage, it can still be used. Cohen describes this as case 2 (Cohen, 1988, p. 202). As the two proportions you can use the sample proportion and the expected proportion. The calculation for h, or h' as he calls it, is then the same as before. However, for the interpretation, we need to multiply the result by the square root of two (Cohen, 1988, p. 203). This gives the rule of thumb shown in Table 2.
| |h'| | Interpretation |
|---|---|
| 0.00 < 0.28 | Negligible |
| 0.28 < 0.71 | Small |
| 0.71 < 1.13 | Medium |
| 1.13 or more | Large |
| Note: Adapted from Statistical power analysis for the behavioral sciences (2nd ed., p. 203) by J. Cohen, 1988, L. Erlbaum Associates. | |
If the expected proportion is 0.5, an alternative effect size could be Cohen g. The Alternative Ratio can also be suitable.
Google adds

