Cohen w
Introduction
Cohen w (Cohen, 1988, pp. 216-252) is an effect size measure that can be used with a goodness-of-fit test that uses a chi-square distribution. It is then the square root out of the test statistic (the chi-square value) divided over the sample size.
Cohen w has the same formula as the Phi Coefficient, which is used as an effect size measure for tests of independence.
Obtaining the Measure
(click below on program of interest to expand)
with Flowgorithm
A basic implementation for Cohen's w in the flowchart in figure 1
Figure 1
Flowgorithm for Cohen's w
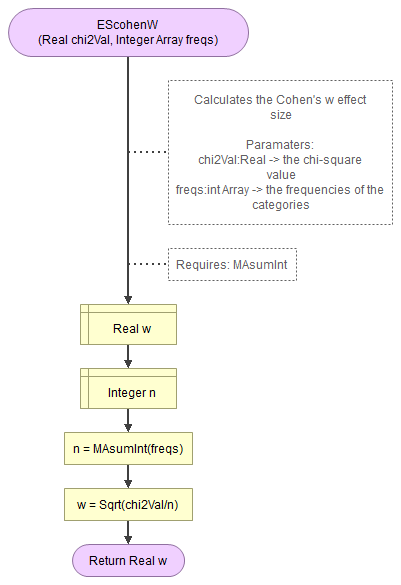
It takes as input the chi-square value, an array of integers with the observed frequencies.
It uses a small helper function to sum an array of integers.
Flowgorithm file: FL-EScohenW.fprg.
with SPSS (not possible?)
To my knowledge it is not possible to determine Cohen's w with SPSS. However, SPSS does return the chi-square value and sample size, so you can use those values with the online calculator below to determine Cohen's w.
SPSS workbook: ES - Cohen w (S).spwb
Online Calculator
Formula
\(w=\sqrt\frac{\chi^{2}}{n}\)
In the above formula \(\chi^2\) is the chi-square test value, \(n\) is the total sample size, and \(k\) is the number of categories.
Given Cramer's V (\(V\)) and the number of categories (\(k\)), the formula for Cohen's w will be:
\(w=V\times\sqrt{k-1}\)
Interpretation
Cohen provided some rule of thumb to interpret this, shown in Table 1.
| w | Interpretation |
|---|---|
| 0.00 < 0.10 | Negligible |
| 0.10 < 0.30 | Small |
| 0.30 < 0.50 | Medium |
| 0.50 or more | Large |
| Note: Adapted from Statistical power analysis for the behavioral sciences (2nd ed., p. 227) by J. Cohen, 1988, L. Erlbaum Associates. | |
Next step and Alternatives
Alternative effect sizes for a Goodness-of-Fit test could be:
If the test is significant a post-hoc analysis to pin-point which category is significantly different could be used. The post-hoc anlysis for a goodness-of-fit test is discussed here.
Google adds

